This all started around a year back, when I got introduced to open source (Free and Open Source, Free as in speech) world. Feeling of being a part of something big was itself amazing and to add someone will be using my work in something great this proved to be more than driving force needed to get me going. The more I worked the more addicted I got. In around October 2015 through my brother and some answers on Quora I came to know about pgmpy(A python library for Probabilistic Graphical Models), and since then I have been contributing continuously. Working with pgmpy have been a great learning experience, I learned lots of new things about python which I didn’t know earlier and of-course Probabilistic Graphical Models. I also came to know about PEP (Python Enhancement Proposals), and especially PEP8 , which made Python code more beautiful to read.

The Proposal

My Proposal deals with adding two new sampling algorithms in pgmpy namely:

• Hamiltonian Monte Carlo or Hybrid Monte Carlo (HMC)
• No U Turn Sampler (NUTS)

If they don’t click anything to you, then no need to worry, even I wasn’t familiar with them before February 2016. Some more blog posts from my side and hopefully you will feel at home with these terms.

These two algorithms have become quite popular in recent time due to there accuracy and speed. Hamiltonian Monte Carlo (HMC) and No U Turn Sampler(NUTS) are Markov chain Monte Carlo (MCMC) algorithms / methods.

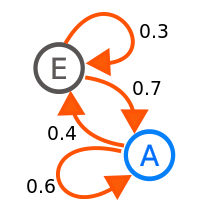
Markov Chains is a transition model with property that the probability distribution of next state in the chain depends on the transition function associated with current state, not the other preceding states in the process. A random walk in Markov Chain gives a sample of that distribution. Markov Chain Monte Carlo sampling is a process that mirrors this behavior of Markov Chain.

Currently pgmpy provides two sampling classes, A range of algorithms namely Forward sampling, Rejection Sampling and Likelihood weighted sampling which are specific to Bayesian Model and Gibbs Sampling a MCMC algorithm that generates samples from both Bayesian Network and Markov models. Hamiltonian/Hybrid Monte Carlo (HMC) is a MCMC algorithm that adopts physical system dynamics rather than a probability distribution to propose future states in the Markov chain. No U Turn Sampler (NUTS) is an extension of Hamiltonian Monte Carlo that does not require the number of steps L (a parameter that is crucial for good performance in case of HMC).

Post Script: When I’ll be finished with my first half of the project I’ll write a series of posts which will serve as an introduction to probabilistic sampling and Markov Chain Monte Carlo, specifically with introduction to Hoeffding’s inequality, Markov Chains, MCMC techniques such as Metropolis-Hastings, Gibbs sampler, and HMC.

References and Links

1. GSoC Proposal
2. Wikipedia, Markov Chain
3. Probabilistic Graphical Models Principles and Techniques: Daphne Koller, Nir Friedman