MCMC: Hamiltonian Monte Carlo and No-U-Turn Sampler

15 Aug 2016

Reading time ~13 minutes

The random-walk behavior of many Markov Chain Monte Carlo (MCMC) algorithms makes Markov chain convergence to target distribution $p(x)$ inefficient, resulting in slow mixing. In this post we look at two MCMC algorithms that propose future states in the Markov Chain using Hamiltonian dynamics rather than a probability distribution. This allows the Markov chain to explore target distribution much more efficiently, resulting in faster convergence.

Hamiltonian Dynamics

Before we move our discussion about Hamiltonian Monte Carlo any further, we need to become familiar with the concept of Hamiltonian dynamics. Hamiltonian dynamics are used to describe how objects move throughout a system. Hamiltonian dynamics is defined in terms of object location $x$ and its momentum $p$ (equivalent to object’s mass times velocity) at some time $t$ . For each location of object there is an associated potential energy $U(x)$ and with momentum there is associated kinetic energy $K(p)$ . The total energy of system is constant and is called as Hamiltonian $H(x, p)$ , defined as the sum of potential energy and kinetic energy:

$H(x, p) = U(x) + K(p)$

The partial derivatives of the Hamiltonian determines how position $x$ and momentum $p$ change over time $t$ , according to Hamiltonian’s equations:

$\frac{dx_i}{dt} = \frac{\partial H}{\partial p_i} = \frac{\partial K(p)}{\partial p_i}$ $\frac{dp_i}{dt} = -\frac{\partial H}{\partial x_i} = -\frac{\partial U(x)}{\partial x_i}$

The above equations operates on a d-dimensional position vector $x$ and a d-dimensional momentum vector $p$ , for $i = 1, 2, \cdots, d$ .

Thus, if we can evaluate $\frac{\partial U(x)}{\partial x_i}$ and $\frac{\partial K(p)}{\partial p_i}$ and have a set of initial conditions i.e an initial position and initial momentum at time $t_0$ , then we can predict the location and momentum of object at any future time $t = t_0 + T$ by simulating dynamics for a time duration $T$ .

Discretizing Hamiltonian’s Equations

The Hamiltonian’s equations describes an object’s motion in regard to time, which is a continuous variable. For simulating dynamics on a computer, Hamiltonian’s equations must be numerically approximated by discretizing time. This is done by splitting the time interval $T$ into small intervals of size $\epsilon$ .

Euler’s Method

The best-known way to approximate the solution to a system of differential equations is Euler’s method. For Hamiltonian’s equations, this method performs the following steps, for each component of position and momentum (indexed by $i=1, ...,d$ )

$p_i(t + \epsilon) = p_i(t) + \epsilon \frac{dp_i}{dt}(t) = p_i(t) - \epsilon \frac{\partial U}{\partial x_i(t)}$ $x_i(t + \epsilon) = x_i(t) + \epsilon \frac{dx_i}{dt} = x_i(t) + \epsilon \frac{\partial K}{\partial p_i(t)}$

Even better results can be obtained if we use updated value of momentum in later equation

$x_i(t + \epsilon) = x_i(t) + \epsilon \frac{\partial K}{\partial p_i(t + \epsilon)}$

This method is called as Modified Euler’s method.

Leapfrog Method

Unlike Euler’s method where we take full steps for updating position and momentum in leapfrog method we take half steps to update momentum value.

$p_i(t + \epsilon / 2) = p_i(t) - (\epsilon / 2) \frac{\partial U}{\partial x_i(t)}$ $x_i(t + \epsilon) = x_i(t) + \epsilon \frac{\partial K}{\partial p_i(t + \epsilon /2)}$ $p_i(t + \epsilon) = p_i(t) - (\epsilon / 2) \frac{\partial U}{\partial x_i(t + \epsilon)}$

Leapfrog method yields even better result than Modified Euler Method.

Example: Simulating Hamiltonian dynamics of a simple pendulum

Imagine a bob of mass $m = 1$ attached to a string of length $l=1.5$ whose one end is fixed at point $(x=0, y=0)$ . The equilibrium position of the pendulum is at $x = 0$ . Now keeping string stretched we move it some distance horizontally say $x_0$ . The corresponding change in potential energy is given by

$U(x) = mg\Delta h$ ,

where $\Delta h$ is change in height and $g$ is gravity of earth.

Using simple trigonometry one can derive relationship between $x$ and $\Delta h$ .

$U(x) = mgl(1 - cos(sin^{-1}(x/l)))$

Kinetic energy of bob can be written in terms of momentum as

$K(v) = \frac{mv^2}{2} = \frac{(mv)^2}{2m} = \frac{p^2}{2m} = K(p)$

Further, partial derivatives of potential and kinetic energy can be written as:

$\frac{\partial U}{\partial x} = \frac{mglx}{\sqrt{l^2 - x^2}}$

and

$\frac{\partial K}{\partial p} = \frac{p}{m}$

Using these equations we can now simulate the dynamics of simple pendulum using leapfrog method in python.

from __future__ import division
import matplotlib.pyplot as plt
import numpy as np

epsilon = 0.025  # Stepsize
num_steps = 98  # No of steps to simulate dynamics
m = 1  # Unit mass
l = 1.5  # length of string
g = 9.8  # Gravity of earth

def K(p):
    return 0.5* (p**2) / m

def U(x):
    epsilon_h = l * (1 - np.cos(np.arcsin(x/l)))
    return m * g * epsilon_h

def dU(x):
    return (m * g * l * x) / (1.5 * np.sqrt(l**2 - x**2))

x0 = 0.4
p0 = 0
plt.ion() ; plt.figure(figsize=(14, 10))
# Take first half step for momentum
pStep = p0 - (epsilon / 2) * dU(x0)
# Take first full step for position
xStep = x0 + epsilon * pStep
# Take full steps
for num_steps in range(num_steps):
    # Update momentum and position
    pStep = pStep - epsilon * dU(xStep)
    xStep = xStep + epsilon * (pStep / m)
    # Display
    plt.subplot(121); plt.cla(); plt.hold(True)
    theta = np.arcsin(xStep / 1.5)
    y_coord = 1.5 * np.cos(theta)
    x = np.linspace(0, xStep, 1000)
    y = np.tan(0.5*np.pi - theta) * x
    plt.plot(0, 0, 'k+', markersize=10)
    plt.plot(x, y, c='black')
    plt.plot(x[-1], y[-1],'bo', markersize=8)
    plt.xlim([-1, 1]); plt.ylim([2, -1]); plt.hold(False)
    plt.title("Simple Pendulum")
    plt.subplot(222); plt.cla(); plt.hold(True)
    potential_energy = U(xStep)
    kinetic_energy = K(pStep)
    plt.bar(0.2, potential_energy, color='r')
    plt.bar(0.2, kinetic_energy, color='k', bottom=potential_energy)
    plt.bar(1.5, kinetic_energy+potential_energy, color='b')
    plt.xlim([0, 2.5]); plt.xticks([0.6, 1.8], ('U+K', 'H'))
    plt.ylim([0, 0.8]); plt.title("Energy"); plt.hold(False)
    plt.subplot(224); plt.cla()
    plt.plot(xStep,pStep,'ko', markersize=8)
    plt.xlim([-1.2, 1.2]); plt.ylim([-1.2, 1.2])
    plt.xlabel('position'); plt.ylabel('momentum')
    plt.title("Phase Space")
    plt.pause(0.005)
# The last half step for momentum
pStep = pStep - (epsilon/2) * dU(xStep)

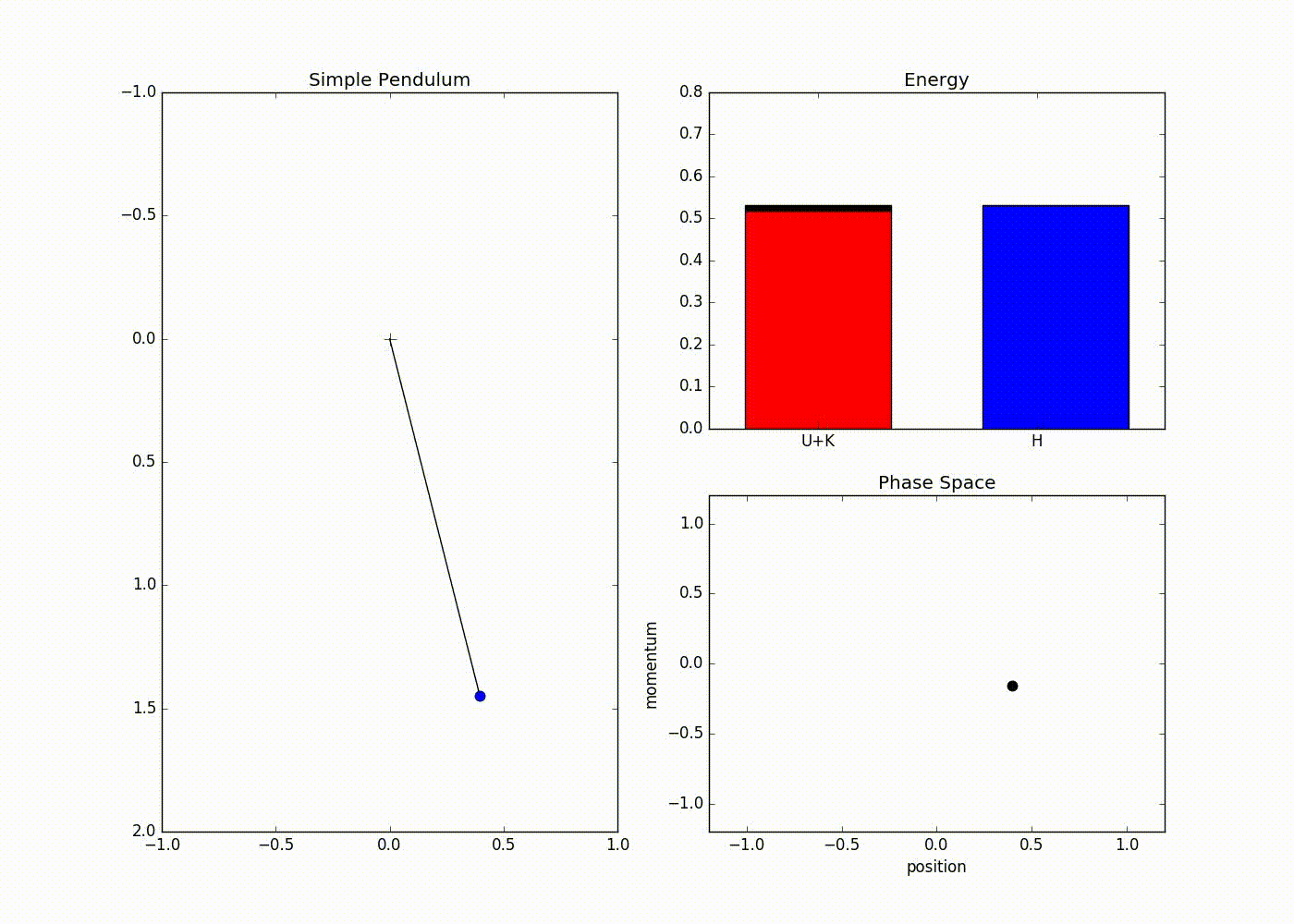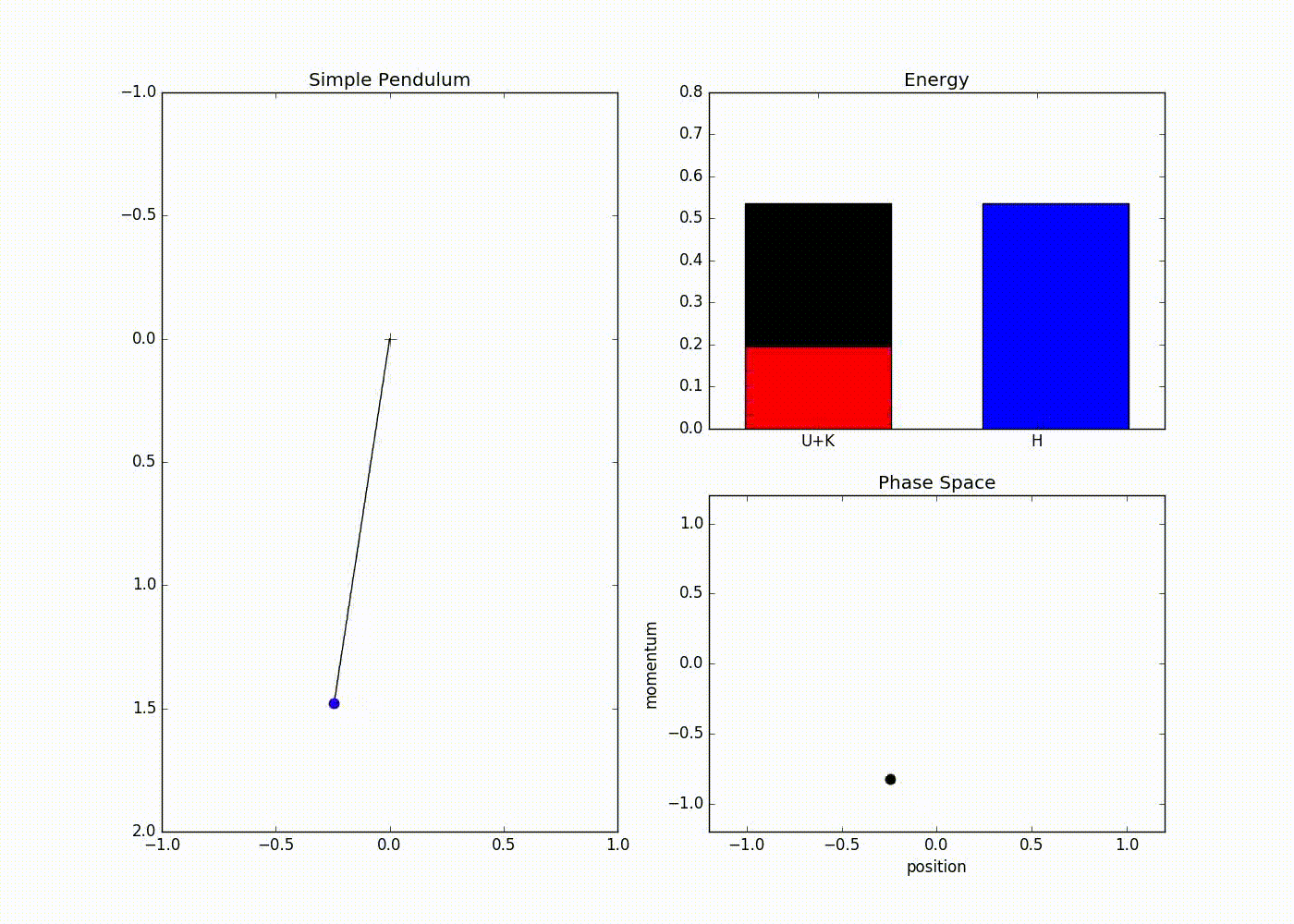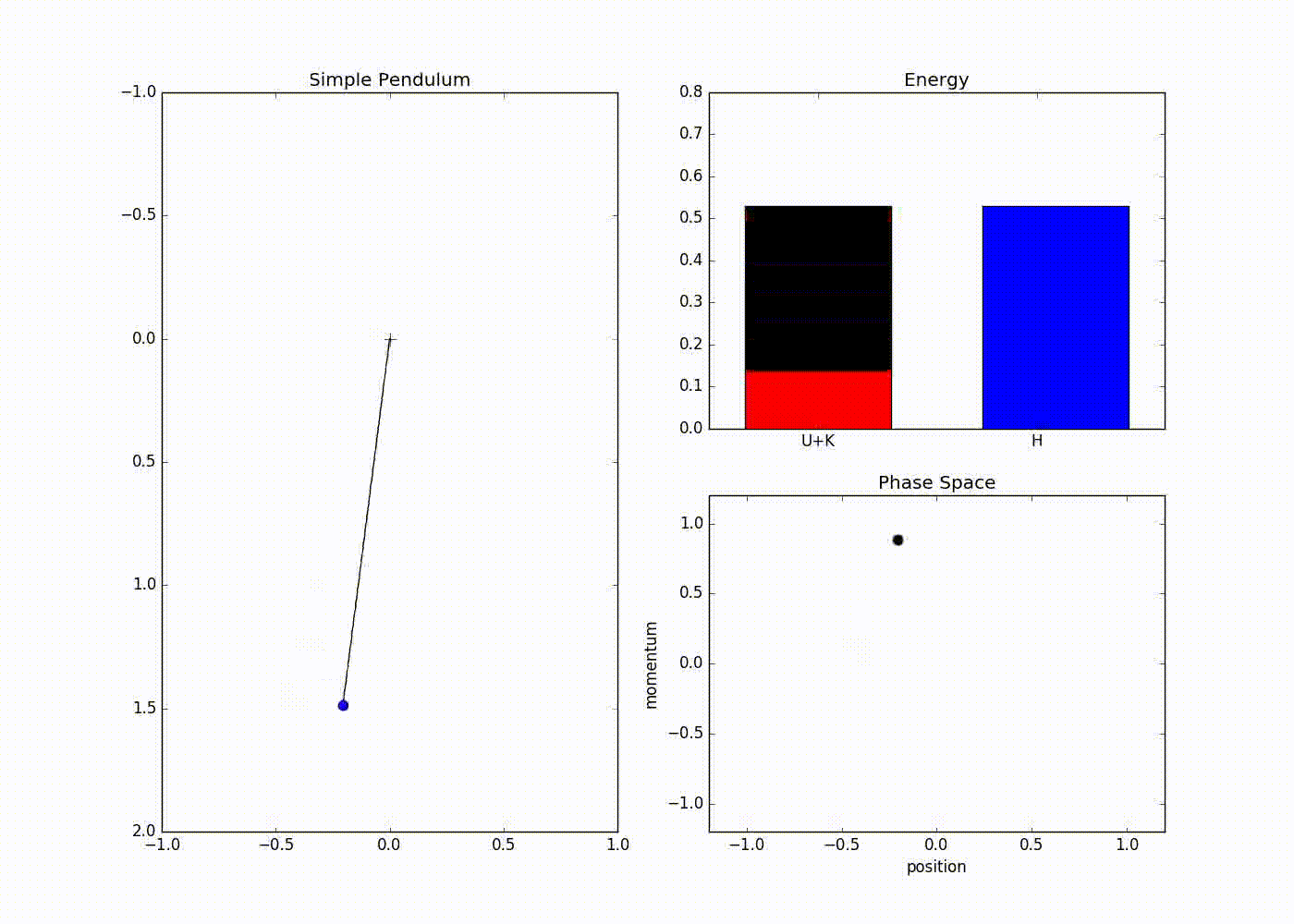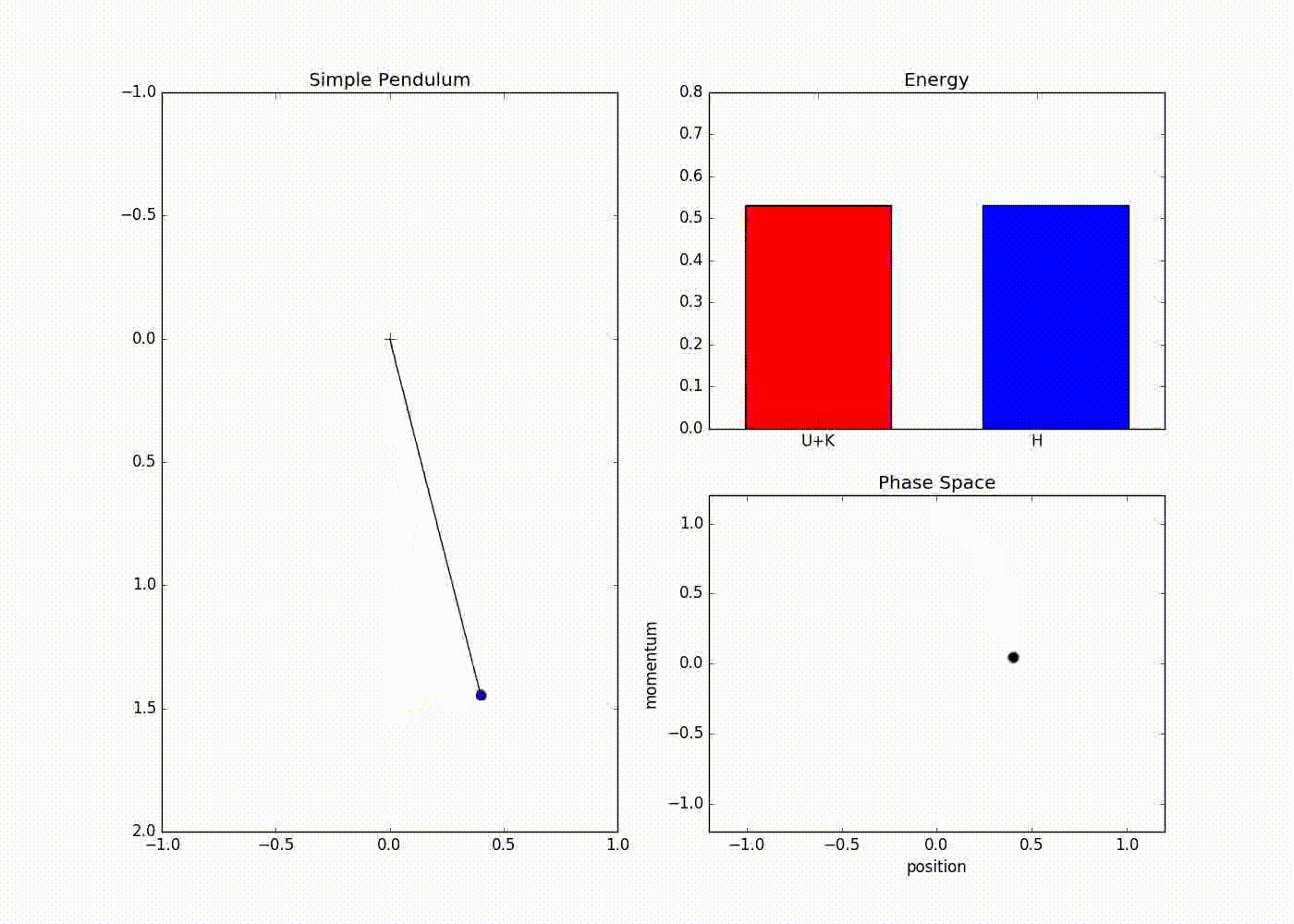
simple pendulum

The sub-plot in the right upper half of the output demonstrates the trade-off between the potential and kinetic energy described by Hamiltonian dynamics. The red portion of first bar plot represents potential energy and black represents kinetic energy. The second bar plot represents the Hamiltonian. We can see that at $x=0$ the potential energy is zero and kinetic energy is maximum and vice-versa at $x=0.4$ . The lower right sub-plot shows the phase space showing how momentum and position are varying. We can see that phase space maps out an ellipse without deviating from its path. In case of Euler method the particle doesn’t fully trace a ellipse instead diverges slowly towards infinity (look at here for further detail).

We can also see that value of Hamiltonian is not constant but is oscillating slightly. This energy drift is due to approximations used to discretize time. One can clearly see that value of position and momentum are not completely random, but takes a deterministic circular kind of trajectory. If we use Leapfrog method to propose future states than we can avoid random-walk behavior which we saw in Metropolis-Hastings algorithm

Hamiltonian and Probability: Canonical Distributions

Now having a bit of understanding what is Hamiltonian and how we can simulate Hamiltonian dynamics, we now need to understand how we can use these Hamiltonian dynamics for MCMC. We need to develop some relation between probability distribution and Hamiltonian so that we can use Hamiltonian dynamics to explore the distribution. To relate $H(x, p)$ to target distribution $P(x)$ we use a concept from statistical mechanics known as the canonical distribution. For any energy function $E(q)$ , defined over a set of variables $q$ , we can find corresponding $P(q)$

$P(q) = \frac{1}{Z} exp \left( \frac{-E(q)}{T} \right)$

, where $Z$ is normalizing constant called Partition function and $T$ is temperature of system. For our use case we will consider $T=1$ .

Since, the Hamiltonian is an energy function for the joint state of “position”, $x$ and “momentum”, $p$ , so we can define a joint distribution for them as follows:

$P(x, p) = \frac{e^{-H(x, p)}}{Z}$

Since $H(x, p) = U(x) + K(p)$ , we can write above equation as

$P(x, p) = \frac{e^{-U(x)-K(p)}}{z}$ $P(x, p) = \frac{e^{-U(x)}e^{-K(p)}}{Z}$

Furthermore we can associate probability distribution with each of the potential and kinetic energy ( $P(x)$ with potential energy and $P(p)$ , with kinetic energy). Thus, we can write above equation as:

$P(x, p) = \frac{P(x)P(p)}{Z'}$

,where $Z'$ is new normalizing constant. Since joint distribution factorizes over $x$ and $p$ , we can conclude that $P(x)$ and $P(p)$ are independent. Because of this independence we can choose any distribution from which we want to sample the momentum variable. A common choice is to use a zero mean and unit variance Normal distribution $N(0, I)$ (look at previous post). The target distribution of interest $P(x)$ from which we actually want to sample from is associated with potential energy.

$U(x) = - log (P(x))$

Thus, if we can calculate $\frac{\partial log(P(x))}{\partial x_i}$ , then we are in business and we can use Hamiltonian dynamics to generate samples.

Hamiltonian Monte Carlo

In Hamiltonian Monte Carlo (HMC) we start from an initial state $(x_0, p_0)$ , and then we simulate Hamiltonian dynamics for a short time using the Leapfrog method. We then use the state of the position and momentum variables at the end of the simulation as our proposed states variables $(x*, p*)$ . The proposed state is accepted using an update rule analogous to the Metropolis acceptance criterion.

Lets look at the HMC algorithm:

Given initial state $x_0$ , stepsize $\epsilon$ , number of steps $L$ , log density function $U$ , number of samples to be drawn $M$

set $m = 0$
repeat until $m = M$
- set $m \leftarrow m + 1$
- Sample new initial momentum $p_0$ ~ $N(0, I)$
- Set $x_m \leftarrow x_{m-1}, x' \leftarrow x_{m-1}, p' \leftarrow p_0$
- repeat for $L$ steps
  - Set $x', p' \leftarrow Leapfrog(x', p', \epsilon)$
- Calculate acceptance probability $\alpha = min \left(1, \frac{exp( U(x') - (p'.p')/2 )}{exp( U(x_{m-1}) - (p_0.p_0)/2 )} \right)$
- Draw a random number u ~ Uniform(0, 1)
- if $u \leq \alpha$ then $x_m \leftarrow x', p_m \leftarrow -p'$

$Leapfrog$ is a function that runs a single iteration of Leapfrog method.

In practice sometimes instead of explicitly giving number of steps $L$ , we use trajectory length which is product of number of steps $L$ , and stepsize $\epsilon$ .

Lets use this HMC algorithm and draw samples from the same distribution multivariate distribution we used in previous post.

$P(x) = N(\mu, \Sigma)$ , where

$\mu = [0, 0]$

and

$\Sigma = \left[ \begin{array}{cc} 1 \qquad 0.97 \newline 0.97 \qquad 1 \end{array} \right]$

I’m going to use HMC implementation from pgmpy, which I have implemented myself.

Here is python code for that

from pgmpy.inference.continuous import HamiltonianMC as HMC, LeapFrog, GradLogPDFGaussian
from pgmpy.factors import JointGaussianDistribution
import numpy as np
import matplotlib.pyplot as plt

np.random.seed(77777)
# Defining a multivariate distribution model
mean = np.array([0, 0])
covariance = np.array([[1, 0.97], [0.97, 1]])
model = JointGaussianDistribution(['x', 'y'], mean, covariance)

# Creating a HMC sampling instance
sampler = HMC(model=model, grad_log_pdf=GradLogPDFGaussian, simulate_dynamics=LeapFrog)
# Drawing samples
samples = sampler.sample(initial_pos=np.array([7, 0]), num_samples = 1000,
                         trajectory_length=10, stepsize=0.25)
plt.figure(); plt.hold(True)
plt.scatter(samples['x'], samples['y'], label='HMC samples', color='k')
plt.plot(samples['x'][0:100], samples['y'][0:100], 'r-', label='First 100 samples')
plt.legend(); plt.hold(False)
plt.show()

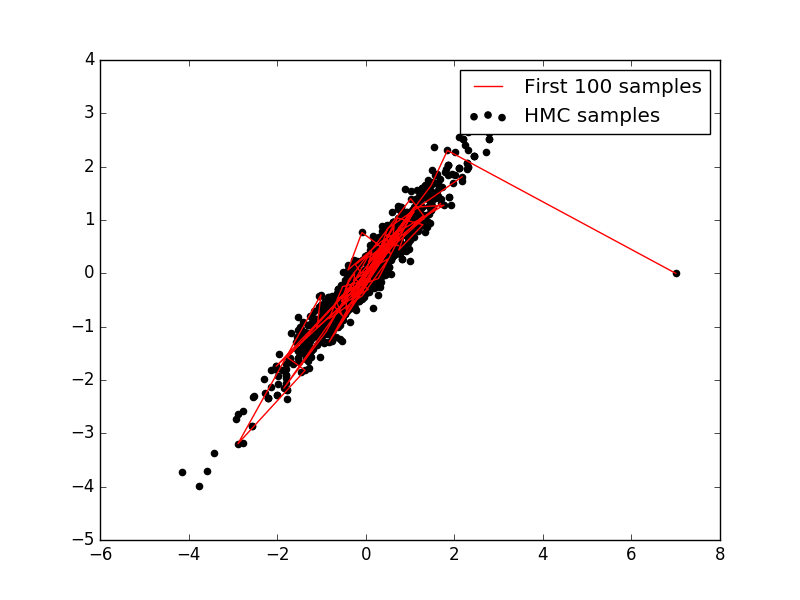
HMC_2D_samples

If one compares these results to what we have seen in previous post for Metropolis-Hastings algorithm it is clear that HMC converges towards target distribution a lot faster than Metropolis-Hastings algorithm. On careful inspection we can also see that graph looks a lot denser than that of Metropolis-Hastings, which mean that our most of the samples are accepted (high acceptance rate).

Though performance of HMC might seem better but it critically depends on trajectory length and stepsize. Poor choice of these can lead to high rejection rate, or too high computation time. One can see the results himself by changing both of the parameters in above example. For example when I just changed stepize to 0.5 from 0.25 in above example, nearly all samples are rejected. Though stepsize parameter for HMC implementation is optional, I do not suggest one should use it.

In pgmpy we have implemented an another variant of HMC in which we adapt the stepsize during the course of sampling thus completely eliminates the need of specifying stepsize (but still requires trajectory length to be specified by user). This variant of HMC is known as Hamiltonian Monte Carlo with dual averaging. In pgmpy we have also provided the implementation of Modified Euler method for simulating Hamiltonian dynamics. (By default both algorithms use Leapfrog. It is not recommended to use Modified Euler method, or Euler method because trajectories are not elliptical, thus they show poor performance in comparison to leapfrog method). Here is a code snippet on how we can use HMCda algorithm in pgmpy.

# Using JointGaussianDistribution from above example
from pgmpy.inference.continuous import HamiltonianMCda as HMCda, ModifiedEuler
# Using modified euler instead of
sampler_da = HMCda(model, GradLogPDFGaussian, simulate_dynamics=ModifiedEuler)
# num_adapt is number of iteration to run adaptation of stepsize
samples = sampler_da.sample(initial_pos=np.array([7, 0]), num_adapt=10,num_samples=10, trajectory_length=10)
print(samples)

Both (HMC and HMCda) of these algorithms requires some hand-tuning from user, which can be time consuming especially for high dimensional complex model. No-U-Turn Sampler (NUTS) is an extension of HMC that eliminates the need to specify the trajectory length but requires user to specify stepsize. With dual averaging algorithm NUTS can run without any hand-tuning at all, and samples generated are at-least as good as finely hand-tuned HMC.

NUTS, removes the need of parameter number of steps by considering a metric to evaluate whether we have ran Leapfrog algorithm for long enough, that is when running the simulation for more steps would no longer increase the distance between the proposal value of $x$ and initial value of $x$

At high level, NUTS uses the leapfrog method to trace out a path forward and backward in fictitious time, first running forwards or backwards 1 step, the forwards and backwards 2 steps, then forwards or backwards 4 steps etc. This doubling process builds a balanced binary tree whose leaf nodes correspond to position-momentum states. The doubling process is halted when the subtrajectory from the leftmost to the rightmost nodes of any balanced subtree of the overall binary tree starts to double back on itself (i.e., the fictional particle starts to make a “U-Turn”). At this point NUTS stops the simulation and samples from among the set of points computed during the simulation, taking are to preserve detailed balance.

The API(in pgmpy) for NUTS and NUTS with dual averaging is quite similar to that HMC. Here is a example

from pgmpy.inference.continuous import (NoUTurnSampler as NUTS, GradLogPDFGaussian,
                                        NoUTurnSamplerDA as NUTSda)
from pgmpy.factors import JointGaussianDistribution
import numpy as np
import matplotlib.pyplot as plt
# Creating model
mean = np.array([0, 0, 0])
covariance = np.array([[6, 0.7, 0.2], [0.7, 3, 0.9], [0.2, 0.9, 1]])
model = JointGaussianDistribution(['x', 'y', 'z'], mean, covariance)
# Creating a sampling instance for NUTS
sampler = NUTS(model=model, grad_log_pdf=GradLogPDFGaussian)
samples = sampler.sample(initial_pos=np.array([1, 1, 1]), num_samples=1000, stepsize=0.4)
# Plotting trace of samples
labels = plt.plot(samples)
plt.legend(labels, model.variables)
plt.title("Trace plot of NUTS samples")
plt.show()

# Creating a sampling instance of NUTSda
sampler_da = NUTSda(model=model, grad_log_pdf=GradLogPDFGaussian)
samples = sampler_da.sample(initial_pos=np.array([0, 1, 0]), num_adapt=1000, num_samples=1000)
# Plotting trace pf samples
labels = plt.plot(samples)
plt.legend(labels, model.variables)
plt.title("Trace plot of NUTSda samples")
plt.show()

The samples returned by all four algorithms are of two types which is dependent upon installation available. If working environment has a installation of pandas, then it will return a pandas.DataFrame object otherwise it will return a numpy.recarry object. As for now pgmpy has pandas as a strict dependency so samples returned would always be a DataFrame object but in near future we will not have pandas as a strict dependency.

Apart from sample method all the four implementation have a another method named generate_sample method, whose each iteration yields a sample which is a simple numpy.array object. This method is useful if one wants to work on a single sample at a time. The API for generate_sample method is exactly similar to that of sample method.

# Using the above sampling instance of NUTSda
gen_samples = sampler_da.generate_sample(initial_pos=np.array([0, 1, 0]),
                                         num_adapt=10, num_samples=10)
samples = np.array([sample for sample in gen_samples])
print(samples)

pgmpy also provides base class structures so that user defined methods can be plugged-in. Lets look at some example on how we can do that. In this example the distribution we are going to sample from is Logistic distribution The probability density of logistic distribution is given by:

$P(x; \mu, s) = \frac{e^{-\frac{x- \mu}{s}}}{s(1 + e^{-\frac{x - \mu}{s}})^2}$

Thus the log of this probability density function (potential energy function) can be written as:

$log(P(x; \mu, s)) = -\frac{x - \mu}{s} - log(s) - 2 log(1 + e^{-\frac{x - \mu}{s}})$

And the gradient of potential energy :

$\frac{\partial log(P(x; \mu, s))}{\partial x} = - \frac{1}{s} + \frac{2e^{-\frac{x - \mu}{s}}}{s(1 + e^{-\frac{x - \mu}{s}})}$

import numpy as np
from pgmpy.factors import ContinuousFactor
from pgmpy.inference.continuous import NoUTurnSamplerDA as NUTSda, BaseGradLogPDF
import matplotlib.pyplot as plt

# Creating a Logistic distribution with mu = 5, s = 2
def logistic_pdf(x):
    power = - (x - 5.0) / 2.0
    return np.exp(power) / (2 * (1 + np.exp(power))**2)
# Calculating log of logistic pdf
def log_logistic(x):
    power = - (x - 5.0) / 2.0
    return power - np.log(2.0) - 2 * np.log(1 + np.exp(power))
# Calculating gradient log of logistic pdf
def grad_log_logistic(x):
    power = - (x - 5.0) / 2.0
    return - 0.5 - (2 / (1 + np.exp(power))) * np.exp(power) * (-0.5)

# Creating a logistic model
logistic_model = ContinuousFactor(['x'], logistic_pdf)

# Creating a class using base class for gradient log and log probability density function
class GradLogLogistic(BaseGradLogPDF):

    def __init__(self, variable_assignments, model):
        BaseGradLogPDF.__init__(self, variable_assignments, model)
        self.grad_log, self.log_pdf = self._get_gradient_log_pdf()

    def _get_gradient_log_pdf(self):
        return (grad_log_logistic(self.variable_assignments),
                log_logistic(self.variable_assignments))

# Generating samples using NUTS
sampler = NUTSda(model=logistic_model, grad_log_pdf=GradLogLogistic)
samples = sampler.sample(initial_pos=np.array([0.0]), num_adapt=10000,
                         num_samples=10000)

x = np.linspace(-30, 30, 10000)
y = [logistic_pdf(i) for i in x]
plt.figure()
plt.hold(1)
plt.plot(x, y, label='real logistic pdf')
plt.hist(samples.values, normed=True, histtype='step', bins=100, label='Samples NUTSda')
plt.legend()
plt.hold(0)
plt.show()

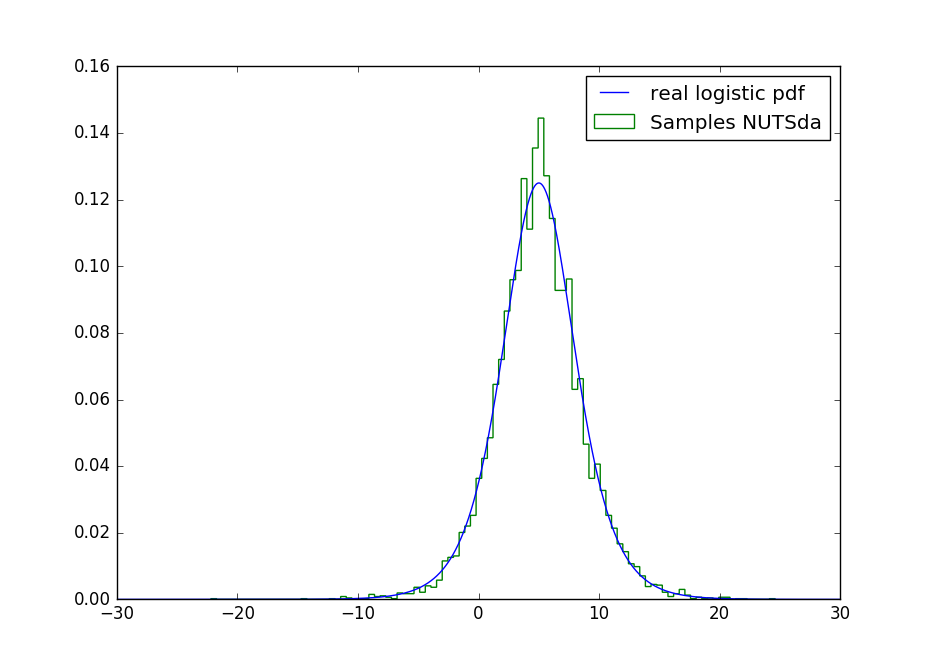
logistics_NUTSda

Ending Note

In this blog we see how by avoid random-walk behavior we can explore target distribution efficiently using some powerful algorithms like Hamiltonian Monte Carlo and No-U-Turn Sampler. In my hopefully next blog post I’ll show not so common yet interesting application of MCMC which I came across recently.